Не так давно в камментах в очередной раз встретил утверждение, что из-за сложности современных экономических отношений ( по улицам курьеры, курьеры, курьеры ... ) они могут регулироваться исключительно "ценовыми сигналами" и в рыночном реактивном (от слова концепции "реакция" т.е. реагирования ) режиме. Т.е. план "невозможен" по техническим причинам - мол невозможно обсчитать. Соответственно и дальше будем ошибаться, а потом исправлять ошибки (невидимой рукой).
Да, плановая экономика невозможна прежде всего из-за пресловутого "пси-фактора" - менеджмент всегда будет грести под себя, "экономические субъекты" будут с азартом топить друг дружку (иногда просто по приколу без всякого win-win) и прч, применять не наилучшие технологии, а ради 300% заниматься хрематистикой - за 5000 лет истории денех, как некоего абсрактного практически "теологического" концепта удачно легшего на хватательные рефлексы высших приматов, ничего не поменялось, но технических проблем сейчас построить что то эффективное не на ценовых сигналах нет. Прогресс вычислительных мощностей и возможностей телекома просто чудовищный.
Для затравки почему "не можно" - еще из прошлого века на эту же тему:

--
Математических моделей для эффективного "не рыночного" управления придумано великое множества (в т.ч. в корп секторе у западоидов не только придумано, но и применяется весь вопрос в размере и структуре контура, которым они управляют, а также его внешних связях), но предлагаю рассмотреть в серии заметок (сам для себя освежу кое что забыл) наиболее известную т.н. "межотраслевой баланс", а также опровергнуть тезис насчет "вычислительной сложности".
Полные исторические справки по Теме легко ищутся в интернете поэтому тут коротко и своими словами (там есть определенная терминология своя - "расширенный баланс", "динамический", "открытый" и прч, ).
Итак рассмотрим "базу" "уравнения" модели отраслевого баланса ( сразу буду описывать не в математических терминах - матрицы, векторы, дифференциалы и прч, а ближе к ИТшым ... массивы и списки - так как аналитически решать ничего не будем ( все же решено до нас, да и алгоритмы особенно работы с матрицами все уже готово ), в итоге попробуем выйти на программную реализацию в т.ч. для упомянутой в обсуждении GPU ( на opencl ) )
1. Концепция затраты-выпуск ( то, за что Леонтьеву нобелевку дали ) ( излагаю своими словами, надеюсь будет понятно )
Входные условия:
(1) ProductionTypes (1..n) - виды продукции в рассматриваемой системе - по сути просто список с наименованиями ( в расчетах не используется )
(2) Потребление ConsumptionVolumes (1..n) - объемы конечного (ну или местами уже конченного) потребления этой продукции потребителями исходя из их фактических потребностей.
(3) Firms(1..n) - список фирм производящих соответствующую продукцию ( производственных единиц, далее обозвали их "отраслями" и прч ) список наименований ( в расчетах не используется )
Матрица технологических возможностей фирм - двухмерный массив
(4) МатрицаВыпуска -FirmsTechnologyMatrix ( 1..n, 1...m ) - со значениями сколько необходимо объемов одной продукции, чтобы получить на выходе единицу выходной продукции
Пример:
Чтобы получить одни штаны необходимо - 4 пуговицы и 2 метра ткани , соответственно в этом участке матрицы в колонках соответствующих фирмам производящим "пуговицы" и "ткань" будет стоять 4 и 2
В массиве потребляемой продукции (2) причем могут быть только штаны т.е. по позициям пуговицы и ткань будет стоять 0 ( таким образом "прячутся" отношения между собой внутри производственного сектора )
Необходимо найти:
(5) Производство - ProductionVolumes (1..n) - объемы _необходимого_ выпуска продукции по видам, чтобы закрыть соответствующие объемы потребления потребителя с учетом фактической матрицы соотношений
Т.е. на практике зная сколько и чего население будет жрать в следующем году и технологические возможности соответствующих "фирм" (отраслей) можно им спустить "план" производства соответствующей продукции, чтобы эти потребности закрыть.
Леонтьев ( на самом деле не совсем он, ну ладно ) выписал уравнение (т.е. переменная в обоих частях )
(6) Производство (5) = МатрицаВыпуска (4) * Производство (5) + Потребление (2)
Которое соответственно в матричном виде решается, как:
(7) Производство = ( ДиагональнаяЕдиничнаяМатрица(МатрицыВыпуска) - МатрицаВыпуска ) ^(-1) * Потребление
пример - продукция - штаны, пуговицы, ткань - фирмы штанин, пуговичкин, тканевой, допустим населению необходимо 5 штанов
Тогда:
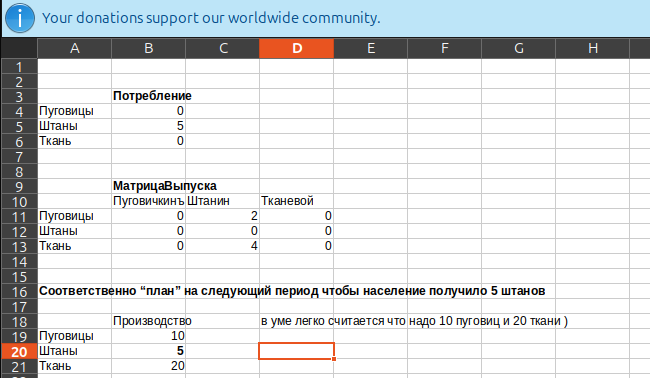
"Матричное" решение
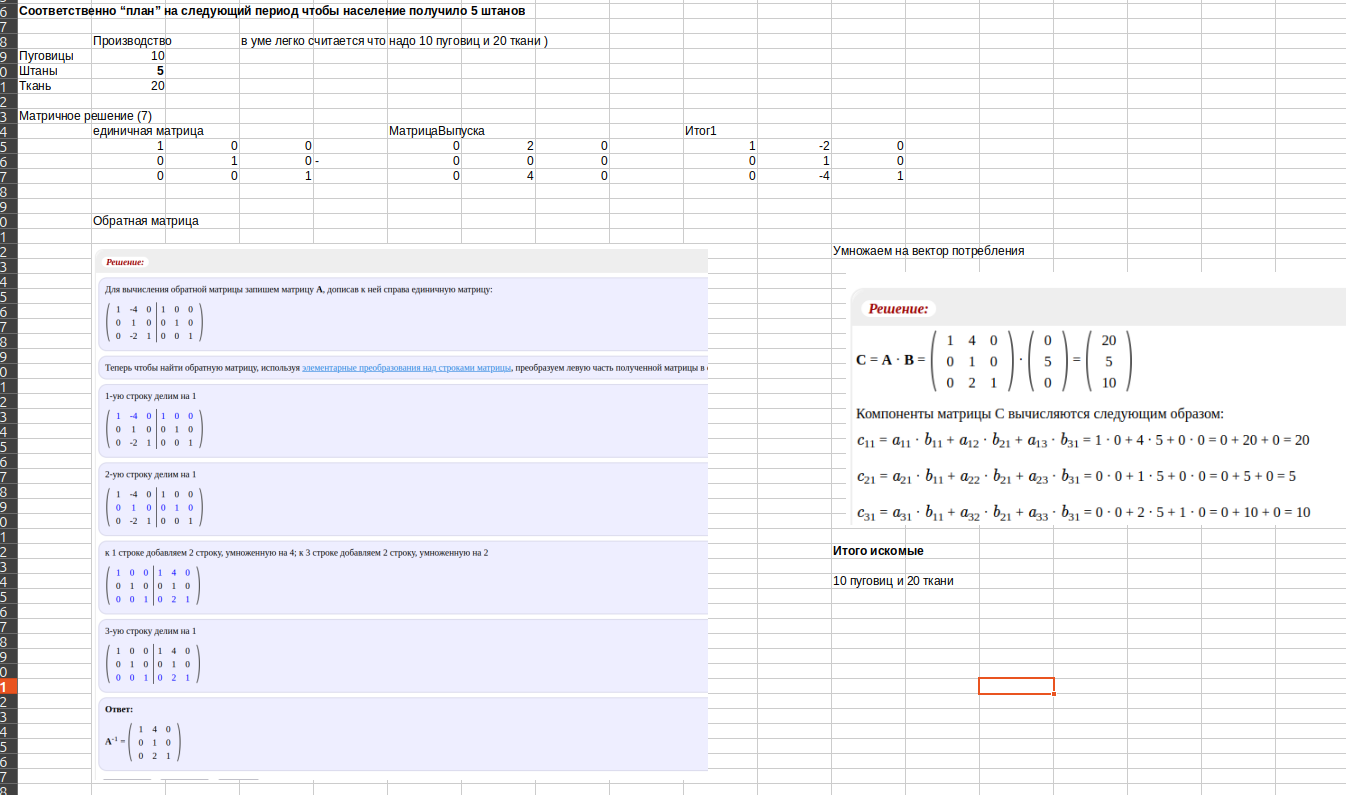
Итого - для пяти штанов для населения необходимо где то взять 10 пуговиц и 20 ткани... главнюки соответственно должен почесать на эту тему репу заранее.
На практике сами понимаете можно различные укрупнения по категоризации брать, но мы сейчас не про практику.
Вроде все понятно написал :) можно на тик ток выложить.
В следующей заметке рассмотрим - расширенный баланс производства с фондами и далее динамический баланс.
P.S.
По камментам - практические вопросы смотрю стали обсуждать - еще рано - это после описания участия денег и вопроса "дискретности" можно только начинать.
На этом этапе можно поднять вопрос о конечной товарной или услуговой "номенклатуре" т.е. списке конечных потребностей у "потребителей" (в обозначениях этой заметки это (1) и (2) ) и тут стоит заметить что это конкретно управляемая структура у тех же западоидов очень все ловко устроено, чтобы ее формировать - там уже и "пре$$а" кстати подключена с контролем внимания и прч..
Красные на этой цепочке провалились почти сразу - "мода" и все такое оно оттуда.